How To Find The Empirical Formula Of A Compound

Affiliate 3. Composition of Substances and Solutions

3.ii Determining Empirical and Molecular Formulas

Learning Objectives

By the finish of this section, yous will be able to:

• Compute the percent composition of a compound
• Determine the empirical formula of a compound
• Decide the molecular formula of a compound

In the previous section, we discussed the relationship between the majority mass of a substance and the number of atoms or molecules it contains (moles). Given the chemical formula of the substance, we were able to determine the amount of the substance (moles) from its mass, and vice versa. But what if the chemic formula of a substance is unknown? In this section, we will explore how to utilise these very aforementioned principles in order to derive the chemical formulas of unknown substances from experimental mass measurements.

Percent Composition

The elemental makeup of a compound defines its chemical identity, and chemical formulas are the most succinct fashion of representing this elemental makeup. When a chemical compound'due south formula is unknown, measuring the mass of each of its elective elements is frequently the starting time step in the procedure of determining the formula experimentally. The results of these measurements allow the calculation of the compound's percent composition, divers as the percentage by mass of each element in the compound. For case, consider a gaseous compound composed solely of carbon and hydrogen. The pct limerick of this chemical compound could be represented as follows:

[latex]\% \;\text{H} = \frac{\text{mass H}}{\text{mass compound}} \times 100 \%[/latex]

[latex]\% \;\text{C} = \frac{\text{mass C}}{\text{mass compound}} \times 100 \%[/latex]

If analysis of a x.0-g sample of this gas showed it to incorporate 2.5 g H and 7.five g C, the pct limerick would be calculated to be 25% H and 75% C:

[latex]\%\;\text{H} = \frac{2.5 \;\text{thou H}}{ten.0 \;\text{one thousand compound}} \times 100 \% = 25 \%[/latex]

[latex]\%\;\text{C} = \frac{7.5 \;\text{g C}}{10.0 \;\text{one thousand chemical compound}} \times 100 \% = 75 \%[/latex]

Example 1

Calculation of Percent Limerick
Analysis of a 12.04-g sample of a liquid chemical compound composed of carbon, hydrogen, and nitrogen showed it to contain 7.34 thou C, i.85 g H, and 2.85 g N. What is the per centum composition of this chemical compound?

Solution
To calculate percent composition, nosotros divide the experimentally derived mass of each element by the overall mass of the chemical compound, and then catechumen to a percentage:

[latex]\%\;\text{C} = \frac{7.34 \;\text{g C}}{12.04 \;\text{g chemical compound}} \times 100\% = 61.0\%[/latex]
[latex]\%\;\text{H} = \frac{1.85 \;\text{g H}}{12.04 \;\text{chiliad compound}} \times 100\% = 15.4\%[/latex]
[latex]\%\;\text{N} = \frac{2.85 \;\text{thousand N}}{12.04 \;\text{grand compound}} \times 100\% = 23.7\%[/latex]

The analysis results indicate that the compound is 61.0% C, 15.4% H, and 23.7% N by mass.

Cheque Your Learning
A 24.81-one thousand sample of a gaseous chemical compound containing only carbon, oxygen, and chlorine is determined to comprise iii.01 k C, four.00 g O, and 17.81 g Cl. What is this compound's percentage composition?

Answer:

12.1% C, 16.1% O, 71.viii% Cl

Determining Pct Composition from Formula Mass

Percent limerick is too useful for evaluating the relative abundance of a given element in different compounds of known formulas. As one example, consider the mutual nitrogen-containing fertilizers ammonia (NH₃), ammonium nitrate (NH₄NO₃), and urea (CH₄N₂O). The element nitrogen is the active ingredient for agricultural purposes, and then the mass percentage of nitrogen in the chemical compound is a practical and economic concern for consumers choosing amongst these fertilizers. For these sorts of applications, the percent composition of a compound is hands derived from its formula mass and the diminutive masses of its elective elements. A molecule of NH₃ contains one N atom weighing 14.01 amu and three H atoms weighing a full of (three × 1.008 amu) = three.024 amu. The formula mass of ammonia is therefore (xiv.01 amu + 3.024 amu) = 17.03 amu, and its percent composition is:

[latex]\%\;\text{Northward} = \frac{fourteen.01 \;\text{amu Northward}}{17.03 \;\text{amu NH}_3} \times 100\% = 82.27\%[/latex]
[latex]\%\;\text{H} = \frac{3.024 \;\text{amu N}}{17.03 \;\text{amu NH}_3} \times 100\% = 17.76\%[/latex]

This same approach may be taken because a pair of molecules, a dozen molecules, or a mole of molecules, etc. The latter amount is almost convenient and would only involve the use of molar masses instead of atomic and formula masses, equally demonstrated Case 2. Equally long as we know the chemic formula of the substance in question, we tin hands derive per centum composition from the formula mass or molar mass.

Example 2

Determining Percent Limerick from a Molecular Formula
Aspirin is a chemical compound with the molecular formula C₉H₈O₄. What is its percent limerick?

Solution
To summate the percent limerick, we need to know the masses of C, H, and O in a known mass of C₉H_eightO₄. Information technology is convenient to consider 1 mol of C_ixH₈O₄ and apply its molar mass (180.159 thou/mole, determined from the chemical formula) to calculate the percentages of each of its elements:

[latex]\begin{array}{r @{{}={}} 50} \%\text{C} & \frac{9 \;\text{mol C} \;\times\; \text{molar mass C}}{\text{molar mass} \;\text{C}_9\text{H}_{18}\text{O}_4} \times 100 = \frac{9 \times 12.01 \;\text{g/mol}}{180.159 \text{thou/mol}} \times 100 = \frac{108.09 \;\text{1000/mol}}{180.159 \;\text{g/mol}} \times 100 \\[1em] \%\text{C} & sixty.00\%\;\text{C} \end{array}[/latex]

[latex]\brainstorm{array}{r @{{}={}} l} \%\text{H} & \frac{eight \;\text{mol H} \;\times\; \text{molar mass H}}{\text{tooth mass} \;\text{C}_9\text{H}_{xviii}\text{O}_4} \times 100 = \frac{eight \times 1.008 \;\text{g/mol}}{180.159 \text{g/mol}} \times 100 = \frac{8.064 \;\text{thou/mol}}{180.159 \;\text{g/mol}} \times 100 \\[1em] \%\text{H} & 4.476\%\;\text{H} \end{array}[/latex]

[latex]\brainstorm{array}{r @{{}={}} fifty} \%\text{O} & \frac{4 \;\text{mol O} \;\times\; \text{tooth mass O}}{\text{molar mass} \;\text{C}_9\text{H}_{eighteen}\text{O}_4} \times 100 = \frac{iv \times xvi.00 \;\text{1000/mol}}{180.159 \text{g/mol}} \times 100 = \frac{64.00 \;\text{g/mol}}{180.159 \;\text{g/mol}} \times 100 \\[1em] \%\text{O} & 35.52\%\;\text{O} \end{array}[/latex]

Note that these percentages sum to equal 100.00% when appropriately rounded.

Cheque Your Learning
To three significant digits, what is the mass percent of atomic number 26 in the compound Fe₂O₃?

Decision of Empirical Formulas

As previously mentioned, the most common approach to determining a compound's chemical formula is to first measure the masses of its constituent elements. Notwithstanding, nosotros must go on in listen that chemic formulas represent the relative numbers, not masses, of atoms in the substance. Therefore, any experimentally derived data involving mass must be used to derive the respective numbers of atoms in the compound. To accomplish this, we can apply molar masses to catechumen the mass of each element to a number of moles. Nosotros then consider the moles of each element relative to each other, converting these numbers into a whole-number ratio that can be used to derive the empirical formula of the substance. Consider a sample of compound determined to contain 1.71 g C and 0.287 one thousand H. The respective numbers of atoms (in moles) are:

[latex]1.17 \;\text{g C} \times \frac{i \;\text{mol C}}{12.01 \;\text{g C}} = 0.142 \;\text{mol C}[/latex]

[latex]0.287 \;\text{g H} \times \frac{1 \;\text{mol H}}{1.008 \;\text{g H}} = 0.284 \;\text{mol H}[/latex]

Thus, nosotros can accurately represent this compound with the formula C_0.142H_0.248. Of course, per accepted convention, formulas contain whole-number subscripts, which tin can exist achieved by dividing each subscript past the smaller subscript:

[latex]\text{C}_{\frac{0.142}{0.142}} \; \text{H}_{\frac{0.248}{0.142}} \;\text{or CH}_2[/latex]

(Recall that subscripts of "ane" are not written just rather assumed if no other number is present.)

The empirical formula for this chemical compound is thus CH₂. This may or non be the compound's molecular formula besides; however, we would need additional information to make that decision (as discussed later in this department).

Consider as another example a sample of compound determined to contain 5.31 g Cl and 8.40 thousand O. Following the aforementioned approach yields a tentative empirical formula of:

[latex]\text{Cl}_{0.150}\text{O}_{0.525} \; = \; \text{Cl}_{\frac{0.150}{0.150}} \; \text{O}_{\frac{0.525}{0.150}} = \text{ClO}_{3.5}[/latex]

In this case, dividing past the smallest subscript withal leaves us with a decimal subscript in the empirical formula. To catechumen this into a whole number, we must multiply each of the subscripts past 2, retaining the same atom ratio and yielding Cl₂O₇ every bit the final empirical formula.

In summary, empirical formulas are derived from experimentally measured element masses past:

1. Deriving the number of moles of each element from its mass
2. Dividing each element's molar corporeality by the smallest tooth amount to yield subscripts for a tentative empirical formula
3. Multiplying all coefficients by an integer, if necessary, to ensure that the smallest whole-number ratio of subscripts is obtained

Figure ane outlines this process in menses chart way for a substance containing elements A and 10.

Figure 1. The empirical formula of a compound can exist derived from the masses of all elements in the sample.

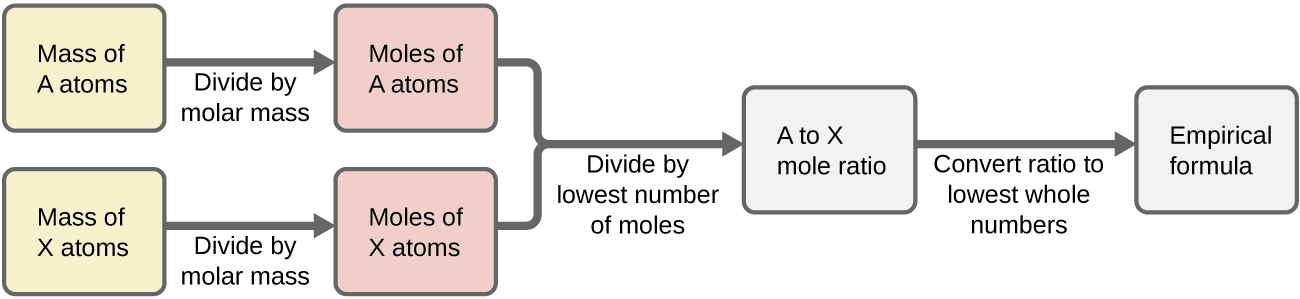
Example three

Determining a Compound'due south Empirical Formula from the Masses of Its Elements
A sample of the black mineral hematite (Figure 2), an oxide of atomic number 26 plant in many iron ores, contains 34.97 g of iron and xv.03 m of oxygen. What is the empirical formula of hematite?

Figure 2. Hematite is an atomic number 26 oxide that is used in jewelry. (credit: Mauro Cateb)

Solution
For this problem, nosotros are given the mass in grams of each chemical element. Begin past finding the moles of each:

[latex]\begin{assortment}{r @{{}={}} 50} 34.97 \;\text{g Atomic number 26} (\frac{\text{mol Fe}}{55.85 \;\text{g}}) & 0.6261 \;\text{mol Atomic number 26} \\[1em] 15.03 \;\text{k O} (\frac{\text{mol O}}{16.00 \;\text{g}}) & 0.9394 \;\text{mol O} \end{array}[/latex]

Next, derive the iron-to-oxygen molar ratio by dividing past the lesser number of moles:

[latex]\begin{array}{r @{{}={}} 50} \frac{0.6261}{0.6261} & ane.000 \;\text{mol Fe} \\[1em] \frac{0.9394}{0.6261} & 1.500 \;\text{mol O} \end{array}[/latex]

The ratio is ane.000 mol of fe to i.500 mol of oxygen (Iron₁O_1.five). Finally, multiply the ratio by two to get the smallest possible whole number subscripts while all the same maintaining the correct fe-to-oxygen ratio:

[latex]two(\text{Fe}_1\text{O}_{1.five}) = \text{Iron}_2\text{O}_3[/latex]

The empirical formula is Iron₂O₃.

Cheque Your Learning
What is the empirical formula of a compound if a sample contains 0.130 g of nitrogen and 0.370 g of oxygen?

For additional worked examples illustrating the derivation of empirical formulas, watch the cursory video prune.

Deriving Empirical Formulas from Percent Composition

Finally, with regard to deriving empirical formulas, consider instances in which a chemical compound's percent composition is bachelor rather than the absolute masses of the compound's constituent elements. In such cases, the percent composition tin be used to calculate the masses of elements present in whatsoever convenient mass of chemical compound; these masses tin can then exist used to derive the empirical formula in the usual fashion.

Determining an Empirical Formula from Percent Composition

Instance 4

The bacterial fermentation of grain to produce ethanol forms a gas with a percent composition of 27.29% C and 72.71% O (Figure iii). What is the empirical formula for this gas?

Effigy three. An oxide of carbon is removed from these fermentation tanks through the large copper pipes at the summit. (credit: "Dual Freq"/Wikimedia Commons)

Solution
Since the scale for percentages is 100, it is well-nigh convenient to calculate the mass of elements present in a sample weighing 100 yard. The adding is "most convenient" because, per the definition for percentage limerick, the mass of a given chemical element in grams is numerically equivalent to the element'due south mass percentage. This numerical equivalence results from the definition of the "pct" unit, whose name is derived from the Latin phrase pct meaning "past the hundred." Considering this definition, the mass percentages provided may be more than conveniently expressed as fractions:

[latex]\begin{array}{r @{{}={}} l} 27.29\% \;\text{C} & \frac{27.29 \;\text{g C}}{100 \;\text{g compound}} \\[1em] 72.71\% \;\text{O} & \frac{72.71 \;\text{g O}}{100 \;\text{g chemical compound}} \cease{array}[/latex]

The molar amounts of carbon and hydrogen in a 100-g sample are calculated by dividing each element's mass past its molar mass:

[latex]\brainstorm{array}{r @{{}={}} l} 27.29\% \;\text{C} (\frac{\text{mol C}}{12.01 \;\text{g}}) & 2.272 \;\text{mol C} \\[1em] 72.71\% \;\text{O} (\frac{\text{mol O}}{16.00 \;\text{g}}) & four.544 \;\text{mol O} \finish{assortment}[/latex]

Coefficients for the tentative empirical formula are derived by dividing each molar amount past the lesser of the two:

[latex]\begin{array}{r @{{}={}} l} \frac{two.272 \;\text{g C}}{2.272} & ane \\[1em] \frac{4.544 \;\text{chiliad O}}{2.272} & two \cease{array}[/latex]

Since the resulting ratio is one carbon to two oxygen atoms, the empirical formula is CO₂.

Check Your Learning
What is the empirical formula of a compound containing 40.0% C, half dozen.71% H, and 53.28% O?

Derivation of Molecular Formulas

Call up that empirical formulas are symbols representing the relative numbers of a compound's elements. Determining the absolute numbers of atoms that compose a unmarried molecule of a covalent compound requires knowledge of both its empirical formula and its molecular mass or molar mass. These quantities may be determined experimentally by diverse measurement techniques. Molecular mass, for example, is often derived from the mass spectrum of the compound (see discussion of this technique in the previous affiliate on atoms and molecules). Tooth mass tin be measured by a number of experimental methods, many of which will be introduced in later chapters of this text.

Molecular formulas are derived by comparing the compound's molecular or tooth mass to its empirical formula mass. Equally the proper noun suggests, an empirical formula mass is the sum of the average diminutive masses of all the atoms represented in an empirical formula. If nosotros know the molecular (or tooth) mass of the substance, we tin split this past the empirical formula mass in order to identify the number of empirical formula units per molecule, which nosotros designate as n:

[latex]\frac{\text{molecular or tooth mass (amu or} \;\frac{\text{k}}{\text{mol}})}{\text{empirical formula mass (amu or} \;\frac{\text{1000}}{\text{mol}})} = n \;\text{formula units/molecule}[/latex]

The molecular formula is then obtained by multiplying each subscript in the empirical formula by n, as shown past the generic empirical formula A_tenB_y:

[latex](\text{A}_{\text{x}} \text{B}_{\text{y}})_{\text{n}} = \text{A}_{\text{nx}} \text{B}_{\text{nx}}[/latex]

For instance, consider a covalent compound whose empirical formula is determined to exist CH₂O. The empirical formula mass for this compound is approximately 30 amu (the sum of 12 amu for one C atom, two amu for two H atoms, and xvi amu for ane O atom). If the compound's molecular mass is determined to be 180 amu, this indicates that molecules of this chemical compound contain 6 times the number of atoms represented in the empirical formula:

[latex]\frac{180 \;\text{amu/molecule}}{30\;\frac{\text{amu}}{\text{formula unit}}} = 6 \;\text{formula units/molecule}[/latex]

Molecules of this compound are then represented by molecular formulas whose subscripts are six times greater than those in the empirical formula:

[latex]\text{(CH}_2\text{O})_6 = \text{C}_6\text{H}_{12}\text{O}_6[/latex]

Notation that this same approach may be used when the molar mass (g/mol) instead of the molecular mass (amu) is used. In this case, we are only considering one mole of empirical formula units and molecules, as opposed to single units and molecules.

Example 5

Determination of the Molecular Formula for Nicotine
Nicotine, an alkaloid in the nightshade family of plants that is mainly responsible for the addictive nature of cigarettes, contains 74.02% C, 8.710% H, and 17.27% N. If 40.57 g of nicotine contains 0.2500 mol nicotine, what is the molecular formula?

Solution
Determining the molecular formula from the provided data will crave comparing of the compound'southward empirical formula mass to its molar mass. Every bit the first step, utilise the percentage composition to derive the compound'south empirical formula. Assuming a user-friendly, a 100-g sample of nicotine yields the post-obit molar amounts of its elements:

[latex]\begin{assortment}{r @{{}={}} fifty} (74.02 \;\text{g C}) (\frac{1 \;\text{mol C}}{12.01 \;\text{thousand C}}) & 6.163 \;\text{mol C} \\[1em] (8.710 \;\text{g H}) (\frac{ane \;\text{mol H}}{i.01 \;\text{one thousand H}}) & 8.624 \;\text{mol H} \\[1em] (17.27 \;\text{chiliad N}) (\frac{1 \;\text{mol North}}{14.01 \;\text{g Due north}}) & one.233 \;\text{mol N} \terminate{array}[/latex]

Adjacent, we calculate the molar ratios of these elements relative to the least abundant chemical element, N.

[latex]\begin{array}{r @{{}={}} fifty} 6.163 \;\text{mol C/} i.233 \;\text{mol N} & v \\[1em] viii.264 \;\text{mol H/} one.233 \;\text{mol N} & 7 \\[1em] 1.233 \;\text{mol N/} ane.233 \;\text{mol N} & i \end{array}[/latex]

[latex]\begin{array}{r @{{}={}} 50} \frac{one.233}{ane.233} & 1.000 \;\text{mol N} \\[1em] \frac{six.163}{1.233} & 4.998 \;\text{mol C} \\[1em] \frac{8.624}{ane.233} & six.994 \;\text{mol H} \end{array}[/latex]

The C-to-N and H-to-N molar ratios are adequately shut to whole numbers, and and so the empirical formula is C₅H_viiNorthward. The empirical formula mass for this compound is therefore 81.13 amu/formula unit, or 81.xiii chiliad/mol formula unit.

Nosotros calculate the molar mass for nicotine from the given mass and tooth corporeality of chemical compound:

[latex]\frac{xl.57 \;\text{thousand nicotine}}{0.2500 \;\text{mol nicotine}} = \frac{162.3 \;\text{g}}{\text{mol}}[/latex]

Comparing the tooth mass and empirical formula mass indicates that each nicotine molecule contains 2 formula units:

[latex]\frac{162.3 \;\text{yard/mol}}{81.xiii \;\frac{\text{g}}{\text{formula unit}}} = 2 \;\text{formula units/molecule}[/latex]

Thus, we can derive the molecular formula for nicotine from the empirical formula by multiplying each subscript by 2:

[latex](\text{C}_5\text{H}_7\text{North})_2 = \text{C}_{10}\text{H}_{14}\text{Due north}_2[/latex]

Check Your Learning
What is the molecular formula of a compound with a per centum composition of 49.47% C, 5.201% H, 28.84% N, and 16.48% O, and a molecular mass of 194.2 amu?

Key Concepts and Summary

The chemical identity of a substance is divers by the types and relative numbers of atoms composing its fundamental entities (molecules in the instance of covalent compounds, ions in the case of ionic compounds). A chemical compound's percentage limerick provides the mass per centum of each element in the compound, and it is ofttimes experimentally determined and used to derive the compound's empirical formula. The empirical formula mass of a covalent chemical compound may be compared to the compound's molecular or molar mass to derive a molecular formula.

Key Equations

• [latex]\%\text{X} = \frac{\text{mass X}}{\text{mass commpound}} \times 100\%[/latex]
• [latex]\frac{\text{molecular or tooth mass ( amu or} \;\frac{\text{1000}}{\text{mol}})}{\text{empirical formula mass ( amu or} \;\frac{\text{g}}{\text{mol}})} = north \;\text{formula units/molecule}[/latex]
• (A_xB_y)_northward = A_nxB_ny

Chemistry Finish of Chapter Exercises

1. What data do we need to make up one's mind the molecular formula of a compound from the empirical formula?
2. Calculate the post-obit to four significant figures:

   (a) the percent composition of ammonia, NH_iii

   (b) the percent composition of photographic "hypo," Na_twoS₂O_iii

   (c) the percent of calcium ion in Ca₃(PO₄)₂

3. Determine the following to four meaning figures:

   (a) the percent composition of hydrazoic acid, HN_iii

   (b) the percent composition of TNT, C_{half dozen}H_ii(CH_iii)(NO₂)_iii

   (c) the percent of And then₄ ^2– in Al₂(SO₄)₃

4. Determine the per centum ammonia, NH_three, in Co(NH₃)_half-dozenCl_iii, to three significant figures.
5. Determine the percent water in CuSO_iv∙5H₂O to three meaning figures.
6. Decide the empirical formulas for compounds with the post-obit percent compositions:

   (a) fifteen.8% carbon and 84.two% sulfur

   (b) forty.0% carbon, half-dozen.seven% hydrogen, and 53.3% oxygen

7. Decide the empirical formulas for compounds with the post-obit pct compositions:

   (a) 43.6% phosphorus and 56.4% oxygen

   (b) 28.7% K, 1.v% H, 22.8% P, and 47.0% O

8. A chemical compound of carbon and hydrogen contains 92.3% C and has a molar mass of 78.1 yard/mol. What is its molecular formula?
9. Dichloroethane, a compound that is frequently used for dry out cleaning, contains carbon, hydrogen, and chlorine. Information technology has a molar mass of 99 g/mol. Analysis of a sample shows that it contains 24.3% carbon and iv.1% hydrogen. What is its molecular formula?
10. Determine the empirical and molecular formula for chrysotile asbestos. Chrysotile has the following percent composition: 28.03% Mg, 21.60% Si, 1.sixteen% H, and 49.21% O. The molar mass for chrysotile is 520.8 one thousand/mol.
11. Polymers are large molecules composed of simple units repeated many times. Thus, they often accept relatively simple empirical formulas. Calculate the empirical formulas of the post-obit polymers:

    (a) Lucite (Plexiglas); 59.9% C, 8.06% H, 32.0% O

    (b) Saran; 24.eight% C, 2.0% H, 73.ane% Cl

    (c) polyethylene; 86% C, xiv% H

    (d) polystyrene; 92.3% C, 7.seven% H

    (e) Orlon; 67.9% C, 5.70% H, 26.four% Due north

12. A major textile dye manufacturer developed a new yellow dye. The dye has a percentage composition of 75.95% C, 17.72% N, and vi.33% H by mass with a molar mass of almost 240 m/mol. Determine the molecular formula of the dye.

Glossary

empirical formula mass

sum of average atomic masses for all atoms represented in an empirical formula

percent composition

percentage by mass of the diverse elements in a compound

Solutions

Answers to Chemical science End of Chapter Exercises

two. (a) % N = 82.24%
% H = 17.76%;
(b) % Na = 29.08%
% South = 40.56%
% O = 30.36%;
(c) % Ca²⁺ = 38.76%

4. % NH_iii = 38.2%

6. (a) CS₂
(b) CH₂O

eight. C₆H_six

x. Mg_threeSi_twoH₃O₈ (empirical formula), Mg₆Si₄H_viO₁₆ (molecular formula)

12. C_xvH₁₅Northward₃

Source: https://opentextbc.ca/chemistry/chapter/3-2-determining-empirical-and-molecular-formulas/

Posted by: joinernessiogs.blogspot.com

Share this post